Objetivo
Nível escolar
8º ano – Ensino Fundamental
Tempo
100 minutos (2 horas/aula de 50 minutos cada)
Conteúdo
Momentos
Introdução: Inicialmente, o (a) professor (a) poderá conversar com os estudantes e ressaltar a importância da utilização do software Geogebra para o desenvolvimento da tarefa. Em seguida, poderá fazer a leitura das questões, chamando a atenção para a sua interpretação e destacando os passos para o desenvolvimento de cada uma delas.
Resolução da tarefa: Para a resolução da tarefa, é interessante que o professor permita que os estudantes dialoguem com os seus pares e utilizem as ferramentas do Geogebra para resolver as questões. Caso se faça necessário, o professor poderá intervir e sanar as possíveis dúvidas, questionando e incentivando os estudantes a buscarem as soluções.
Socialização: Por fim, o professor poderá socializar aos estudantes que eles apresentem as soluções das questões da tarefa, retomando o desenvolvimento de toda a tarefa e perguntando a cada grupo o que eles perceberam com o estudo de ângulos externos, as dificuldades que tiveram na investigação dos ângulos e a característica principal que os estudantes perceberam ao estudar esse conteúdo.
Sistematização: O professor poderá retomar a tarefa revisando a classificação dos triângulos quanto aos lados e aos ângulos, discutindo o conceito de ângulos externos e as conclusões que obtiveram a cerca da medida da soma dos ângulo externos.
Recursos
Tarefa; Software Geogebra, lápis, borracha, datashow e lousa digital (opcional).

Todo conteúdo do ambiente está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional. agora só falta o php
A IMPLEMENTAÇÃO DE UMA TAREFA SOBRE ÂNGULOS EXTERNOS DE UM TRIÂNGULO COM O SOFTWARE GEOGEBRA
Profa. Mércia Cleide Barbosa Mota de Sousa
A presente narrativa tem como objetivo descrever uma tarefa realizada em uma turma do 9º ano do Ensino Fundamental do turno vespertino do Colégio Estadual General Osório, localizado no município de Feira de Santana-Ba em 2013. Participaram da tarefa 22 estudantes com faixa etária entre 13 e 16 anos.
Essa tarefa teve como objetivo reconhecer e representar os ângulos externos de um triângulo, assim como sua soma. Para a implementação da tarefa, utilizei o software Geogebra[1] e antes de desenvolvê-la, promovi um encontro de familiarização para que os estudantes conhecessem as ferramentas disponíveis e tivessem mais habilidade para manusear o software.
Inicialmente, planejei a implementação de forma que cada estudante tivesse acesso a um computador, contudo por motivos técnicos (a escola não possuía a quantidade suficiente de computadores funcionando), os estudantes foram remanejados e distribuídos em duplas e trios para utilização de cada equipamento. Para a realização da tarefa, os estudantes foram organizados em oito duplas e dois trios na sala de informática, sendo utilizadas duas aulas de cinquenta minutos cada.


Figura 1: Organização da turma para a implementação da tarefa
No primeiro momento, conversei com os estudantes sobre a importância da utilização do software na tarefa. Em seguida, projetei a tela inicial do Geogebra na lousa digital e distribui a folha da tarefa para os grupos, fazendo a leitura da primeira questão. Posteriormente, solicitei que lessem novamente para que pudessem responder, pois continha muitas informações. No momento seguinte, os estudantes em grupo começaram a resolução da questão 1. Ao acompanhar as equipes, percebi que houve uma dúvida inicial na sua interpretação. Como os estudantes já tinham conhecimento dos ângulos internos, somaram suas medidas, sem observar que a questão fazia referência aos ângulos externos. Então, solicitei novamente que os estudantes fizessem uma nova leitura.
Ainda na primeira questão, percebi que a maioria dos grupos estava com dúvidas no que se refere à medição dos ângulos externos. Por conta disso, fiz a leitura da questão: Construa no software Geogebra um triângulo e nomeio de ABC. Depois, trace uma reta definida por dois pontos que passe pelos vértices A e B deste triângulo. Sobre essa reta, construa um ponto fora do triângulo de modo que ele esteja mais próximo do vértice B e nomeio de D. Em seguida, marque e meça o ângulo formado pelos segmentos DB e BC. O que podemos observar?
Em seguida, com o intuito de sanar as dúvidas dos estudantes quanto à construção requerida nessa questão, utilizei a projeção do software para construir o triângulo, a reta, o ponto e o ângulo externo que a mesma solicitava. [Vídeo 1] Após a minha intervenção, os estudantes conseguiram realizar a construção e resolver a questão 1.
No momento seguinte, os estudantes continuaram respondendo a tarefa e passaram para a questão dois. Nessa questão, algumas duplas não conseguiram associar a construção do triângulo realizada anteriormente e, ao tentarem encontrar o ângulo externo, marcavam outro ângulo, o qual pode ser observado na figura abaixo.
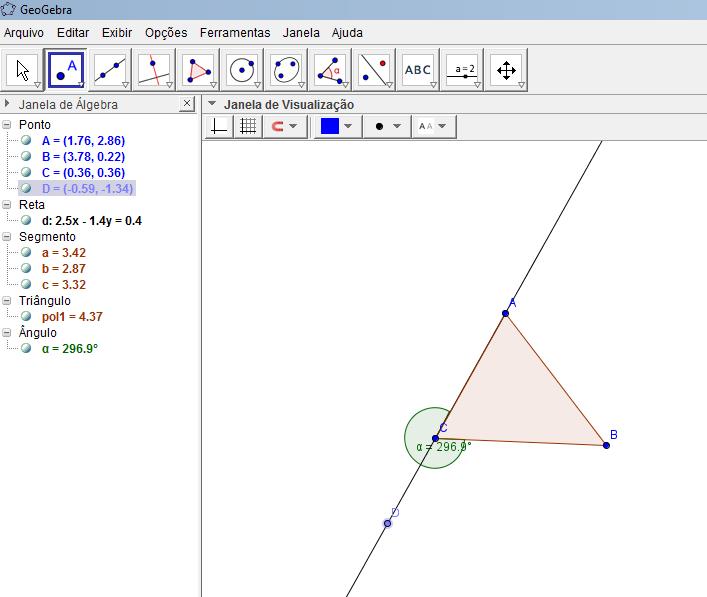
Figura 2: Tentativa de identificar o ângulo externo
Diante disso, percebi que os estudantes ainda não compreendiam o conceito de ângulo externo. Nesse momento, fez-se necessário minha intervenção nos grupos levando-os a investigar como reconhecer o ângulo externo. [Vídeo 2]
Após a compreensão do conceito de ângulo externo, os estudantes passaram a construir os três triângulos quaisquer, como solicitado na questão 2, e encontraram os ângulos externos. Esse momento pode ser observado no diálogo abaixo:
Professora: A partir daí, vocês observaram o quê nessa questão 2, principalmente?
Vocês disseram que sentiram dificuldades? O que vocês observaram nestes três triângulos aí?
Estudante: Que todos os triângulos medem 360º [referindo-se à soma dos ângulos externos de um triângulo]
Professora: Todos os triângulos medem 360°. E dentro disso aí, vocês entenderam agora o que é ângulo externo? Qual a característica principal?
Estudante: Que todos os triângulos medem 360° [referindo-se à soma dos ângulos externos de um triângulo]
Professora: OK!
Nesse momento, foi importante destacar que estávamos nos referindo à soma das medidas dos ângulos externos de cada triângulo para que os estudantes compreendessem essa característica. Nesta mesma questão, ao prolongar os lados dos triângulos, as retas se interceptavam confundindo um pouco os estudantes. Então, sugeri que os triângulos fossem construídos em telas separadas para que reconhecessem os ângulos externos de forma mais clara e consequentemente, a sua soma.
Na terceira questão, percebi que ocorreu um processo de investigação quando os estudantes deformaram os triângulos e associaram suas características (com relação aos lados e ângulos) à soma dos ângulos externos. Foi um momento importante, porque os estudantes estavam tentando colocar o vértice em uma posição em que os ângulos do triângulo ficassem iguais. Mesmo assim, a maioria dos grupos conseguiu construir os triângulos equilátero e isósceles sem maiores dificuldades. Ao dar continuidade a questão 3, a qual também propunha que deformassem os triângulos retângulo e acutângulo, os estudantes não tiveram dificuldades e imediatamente concluíram que, independentemente do tipo de triângulo, a soma dos ângulos externos era 360º.
Ao passo que os estudantes foram terminando a tarefa, comecei a perguntar em cada grupo: o que vocês perceberam com o estudo de ângulos externos? Qual foi a dificuldade que tiveram com esse estudo? Qual a característica principal que vocês perceberam com o estudo dos ângulos externos? [Vídeo 3]
Em seguida, realizei a sistematização da tarefa, revisando a classificação dos triângulos quanto aos lados e ângulos, discutindo com os grupos o conceito de ângulo externo e as conclusões que obtiveram acerca da sua soma. Nesse momento, os estudantes ficaram à vontade para socializar com turma o que haviam compreendido sobre a tarefa. [Vídeo 4]
Para finalizar, agradeci a turma pela participação e recolhi os registros escritos. Assim, considero de suma importância a implementação da tarefa sobre ângulos externos, uma vez que os estudantes ainda não tinham estudado esse tópico de geometria. Nesse sentido, a partir da construção e posterior investigação, os estudantes foram desafiados a compreender o conceito de ângulo externo e concluir que, independentemente da classificação dos triângulos (no que se refere aos lados e aos ângulos), a soma dos ângulos externos não se altera. Desse modo, a tarefa vivenciada foi relevante, pois foi um momento que propiciou investigação, discussão, interação, motivação e reflexão na aula.
[1]Trata-se de um programa livre, desenvolvido por MarkusHohenwarter, disponível, em português, no endereço eletrônico http://www.geogebra.at/
|
Você pode usar, transformar e compartilhar este material que registou uma aula cujo objetivo foi ensinar classificação de quadriláteros e suas propriedades. Você pode fazer mais! Pode contribuir com este material, enviando:
Para contribuir, você deve enviar o arquivo, em formado “.doc”, para este e-mail: educacaomatematica@ufba.br. No corpo da mensagem, informe seu nome completo, instituição, série a que se refere o material enviado, cidade, estado e país. O Observatório da Educação Matemática publicará sua contribuição na janela correspondente ao assunto, de modo que todos os visitantes do ambiente possam ter acesso. |
 |
EXPLANAÇÃO DE COMO CONSTRUIR UM ÂNGULO EXTERNO NO SOFTWARE GEOGEBRA
Este vídeo apresenta o momento em que a professora, ao perceber que os estudantes apresentavam algumas dúvidas em relação aos procedimentos e ferramentas do software (as quais deveriam ser usados para resolver a primeira questão), decidiu resolver a primeira questão chamando atenção para os passos necessários para a construção do ângulo externo do triângulo. Essa explanação norteou os estudantes para que compreendessem como encontrar o ângulo externo e para que tivessem subsídios para responder as questões seguintes. Sugerimos que no momento da familiarização com o software, o(a) professor(a) não apenas trabalhe a utilização das ferramentas, mas que também crie situações para que os estudantes percebam as potencialidades de cada ferramenta.
COMO UM ESTUDANTE EXPLICOU A CONSTRUÇÃO DOS ÂNGULOS EXTERNOS?
Nesse vídeo, o estudante explicou os passos para construção dos ângulos externos do triângulo. Percebe-se que durante a resolução da tarefa, esse estudante conseguiu encontrar os ângulos externos de um triangulo e concluiu que a soma desses ângulos é 360°. Sugerimos que o(a) professor(a) instigue os estudantes a relatarem sobre a forma de resolver a questão, afim de que eles compreendam melhor os conceitos propostos.
SISTEMATIZAÇÃO DA TAREFA: FEEDBACK ENTRE A PROFESSORA E ESTUDANTES
Esse vídeo mostra o momento de sistematização em que a professora interagiu com um dos grupos e lançou questões chave, para que os estudantes sintetizem algumas ideias a respeito de ângulos externos. Esse feedback é importante para que o(a) professor(a) perceba se os estudantes conseguiram entender o conteúdo explorado na tarefa. Uma sugestão é que o(a) professor(a) tente sistematizar com todas as duplas e, posteriormente, abra para uma discussão coletiva em que seja discutido os pontos mais relevantes.
SISTEMATIZAÇÃO E SOCIALIZAÇÃO DA TAREFA
Esse vídeo evidenciou um momento de socialização e sistematização coletiva, em que a professora, primeiramente, retomou algumas características em relação a lados e ângulos dos triângulos, até chegar a construção e compreensão dos ângulos externos. Em seguida, alguns estudantes falam sobre a importância da tarefa, e destacam que o uso do software Geogebra tornou a aula mais dinâmica. Esse momento foi importante porque propiciou uma reflexão sobre a característica dos ângulos externos e abriu espaço, para que outros trabalhos dessa natureza sejam desenvolvidos em sala.