Objetivo
Nível escolar
8º ano –Ensino Fundamental
Tempo
150 minutos (3 horas/aula de 50 minutos cada)
Conteúdo
Momentos
Introdução: Professor(a), sugerimos que antes de realizar a leitura da tarefa, enfatize a importância da atenção deles neste momento, para que eles possam responder as questões da tarefa. Leia a tarefa e conceda aos estudantes um espaço de tempo para que eles possam construir as figuras solicitadas na malha do software Geogebra. É importante mantê-los focados nos procedimentos a serem realizados para dinamizar a implementação da tarefa.
Resolução da tarefa: Após entregar a tarefa, converse com os estudantes a respeito do software Geogebra, pois será preciso que os mesmos tenham uma familiaridade com os ícones básicos do software que serão utilizados para construir as figuras solicitadas para a resolução das questões da tarefa. Depois do tempo concedido para que os estudantes tracem as figuras, leia a primeira questão e dê um tempo para eles responderem, acompanhando com intervenções para esclarecer dúvidas, mas não prejudique o caráter exploratório da tarefa. Outra sugestão é solicitar aos estudantes que levem uma calculadora para que realizem as somas relacionadas às medidas dos ângulos complementares e suplementares, confrontando com os valores demonstrados na janela de álgebra no software Geogebra.
Socialização: Professor(a), discuta com os estudantes a respeito das respostas deles, esclarecendo dúvidas que porventura persistirem durante a resolução da tarefa.
Sistematização: Professor (a), sugerimos que sistematize o conteúdo por questão, afim de que os estudantes não se confundam nos conceitos abordados.
Recursos
Tarefa; lápis, borracha; software Geogebra.

Todo conteúdo do ambiente está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional. agora só falta o php
CONSTRUINDO E RECONHECENDO ÂNGULOS CONSECUTIVOS, ADJACENTES, COMPLEMENTARES E SUPLEMENTARES NO ENSINO FUNDAMENTAL
Sofia Marinho da Natividade
O objetivo deste texto é narrar a implementação de uma tarefa sobre a exploração de ângulos, em particular, ângulos consecutivos e adjacentes, complementares e suplementares, realizada em 2013. A tarefa foi implementada em uma turma de 8º ano do Ensino Fundamental, composta por 25 estudantes com idades entre 14 e 16 anos, da Escola Estadual Ernestina Carneiro, situada em um bairro da periferia da cidade de Feira de Santana-Bahia. Nessa tarefa, os (as) estudantes foram convidados (as) a construir e reconhecer ângulos consecutivos, adjacentes, complementares e suplementares.
Durante a implementação da tarefa, foi utilizado o software Geogebra, um programa de Geometria dinâmica que permite realizar construções geométricas com a utilização de pontos, retas, segmentos de reta, polígonos, dentre outros. O programa reúne ferramentas que auxiliam os estudantes em construções geométricas e, ao mesmo tempo, no trabalho com a álgebra e geometria.
Iniciei a aula com algumas considerações a respeito do software Geogebra, cujo contato ocorreu em encontros anteriores promovidos por mim. Esses encontros foram necessários para que a turma se familiarizasse com alguns ícones e comandos do software que seriam utilizados na tarefa. Li a primeira questão e pedi para os estudantes atentassem para a questão, pois os procedimentos realizados naquele momento seriam importantes para a resolução da mesma. Nesse momento, solicitei que, partindo de um ponto comum, traçassem três semirretas definidas por dois pontos, nomeassem o ponto de encontro dessas três semirretas e as demais semirretas, além disso, que identificassem os três ângulos formados pelas semirretas e o que poderia ser afirmado a respeito desses ângulos [Vídeo 1].
.jpg)
Figura 1: Leitura da tarefa pela professora
Para realizar esses procedimentos, os estudantes localizaram no software Geogebra os ícones que lhes possibilitaram construir as três semirretas solicitadas, levando à formação de três ângulos que foram identificados com facilidade de acordo com as letras que cada um escolheu para renomear.
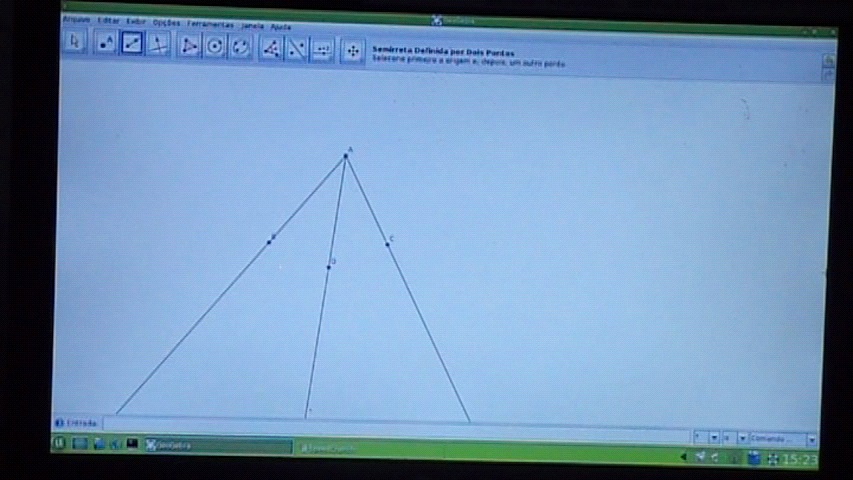
Figura 2: Construção de ângulos consecutivos e adjacentes
Foi dado um tempo para que realizassem os procedimentos e na sequência perguntei: O que podemos afirmar a respeito desses ângulos?
Os estudantes olharam-me com certo ar de indecisão, talvez por não terem tido contato com o conteúdo apresentado ou por não conseguirem expressar a relação de vizinhança entre os ângulos. Então, fui até a lousa da sala e tracei uma figura semelhante à que eles haviam traçado para dar uma orientação sobre a questão. Assim, comecei a questioná-los sobre a semelhança entre a minha figura com a que eles construíram. Em seguida, mostrei aos estudantes que, na figura, poderíamos encontrar três ângulos. A partir daí, eles começaram a identificar os ângulos nas suas próprias representações [Vídeo 2].
Aproveitando o entendimento dos estudantes acerca dos ângulos construídos, questione-os sobre a posição dos ângulos, ou seja, se eles se encontravam juntos ou separados e se existiam algo em comum entre eles. Nesse momento, iniciei a abordagem sobre ângulos consecutivos e adjacentes e expliquei que dois ângulos são consecutivos quando possuem o mesmo vértice e um lado comum. E que dois ângulos consecutivos que não possuem pontos internos comuns são denominados adjacentes. Pedi que cada estudante identificasse os ângulos consecutivos e adjacentes em suas respectivas construções. Aproveitei o momento para reforçar a definição de ângulos consecutivos e adjacentes e, em seguida, solicitei que escrevessem tudo que havíamos discutido sobre tais ângulos. Os estudantes demoraram um pouco, mas conseguiram responder a primeira questão [Vídeo 3].
Na segunda questão, eles conseguiram realizar os procedimentos corretamente, ou seja, construíram no software Geogebra dois ângulos, um medindo 90° e outro medindo 180°, e uma semirreta interna a cada um deles. Além disso, responderam o que poderia ser afirmado a respeito da soma das medidas desses ângulos. Todavia, uma inquietação era como introduzir os termos complementares e suplementares.
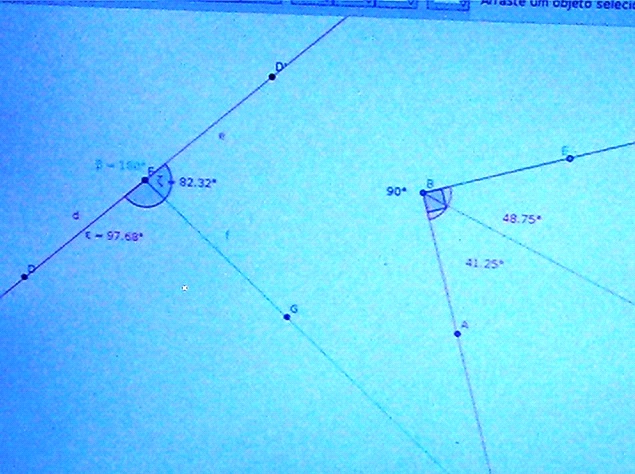
Figura 3: Construção de ângulos complementares e suplementares
O procedimento foi o mesmo utilizado para responder a primeira questão. Na lousa, construí dois ângulos, um com medida de 90° e outro medindo 180°, tracei uma semirreta interna a cada um desses ângulos, partindo do vértice e comecei questionar os estudantes a respeito das medidas encontradas em cada ângulo depois que as semirretas foram traçadas [Vídeo 4]. Ao meu pedido, os estudantes as movimentaram e observaram se a soma das medidas dos ângulos era alterada e concluíram que não.
Apesar dos ângulos internos a eles terem valores diferentes, a soma resultava respectivamente em 90°, no caso de ângulos complementares, e 180° com os suplementares [Vídeo 5].
Nesse momento, salientei aos estudantes que dois ângulos adjacentes cuja soma de suas medidas é igual a 90° são denominados de complementares, e se a soma das medidas for igual a 180° são denominados de suplementares. Fizemos alguns exemplos análogos às construções no software Geogebra e sistematizamos para cada ângulo, expondo o que eles tinham visto durante a aula. Com isso, eles interagiram apresentado suas respostas, de modo que as dúvidas fossem sanadas [Vídeo 6].
Gostaria de salientar que esta tarefa foi implementada em uma turma que não havia estudado o conteúdo ângulos consecutivos, adjacentes, complementares e suplementares. Os estudantes não demonstraram dificuldades em manusear o software, mas sim em registar no papel o que eles verbalizavam. O fato de trabalharem em duplas, em função da disponibilidade de computadores da nossa sala de informática, contribuiu para que os estudantes compartilhassem ideias e estratégias, tornando a aula mais dinâmica.
×|
Você pode usar, transformar e compartilhar este material que registou uma aula cujo objetivo foi ensinar classificação de quadriláteros e suas propriedades. Você pode fazer mais! Pode contribuir com este material, enviando:
Para contribuir, você deve enviar o arquivo, em formado “.doc”, para este e-mail: educacaomatematica@ufba.br. No corpo da mensagem, informe seu nome completo, instituição, série a que se refere o material enviado, cidade, estado e país. O Observatório da Educação Matemática publicará sua contribuição na janela correspondente ao assunto, de modo que todos os visitantes do ambiente possam ter acesso. |
 |
INTRODUÇÃO DA TAREFA
Nesse vídeo, a professora inicialmente fez menção ao software Geogebra que seria utilizado na resolução da tarefa. Em seguida, fez leitura da primeira questão solicitando a atenção dos estudantes. O objetivo desta estratégia foi que os estudantes compreendessem quais os procedimentos seriam necessários para o desenvolvimento da tarefa, desde a construção no software Geogebra de um ponto comum, de onde partiriam três semirretas que seriam renomeadas até a identificação dos ângulos formados por elas. Sugerimos que o(a) professor(a) relembre intuitivamente a definição de um ponto comum utilizando um exemplo prático para que os estudantes compreendam melhor o que farão na questão.
CONSTRUÇÃO DAS TRÊS SEMIRRETAS
Nesse vídeo, os estudantes utilizaram os ícones do software Geogebra para construir as três semirretas, partindo de um ponto comum como solicitado na questão. Aqui, é possível perceber a autonomia dos estudantes na utilização do software Geogebra . Apesar disso, a professora não deixou de mediar esse processo, incentivando-os a dar continuidade aos procedimentos solicitados, visando uma maior exploração da tarefa e das ferramentas do software.
RETOMANDO OS PROCEDIMENTOS REALIZADOS
Nesse vídeo, a professora retomou os procedimentos que foram realizados na primeira questão e sistematizou. Ela observou algumas construções no software Geogebra com o intuito de verificar se os estudantes estavam conseguindo acompanhar a resolução da questão. Além disso, a professora esboçou na lousa um gráfico similar às construções feitas, ressaltando a diferença nas letras que eles utilizaram para renomear os pontos. Essa estratégia teve como objetivo reforçar a identificação e definição dos ângulos consecutivos e adjacentes, visando um melhor entendimento por partes dos estudantes. Sugerimos que o(a) professor(a) enfatize no decorrer da sistematização que todo ângulo adjacente é também um ângulo consecutivo.
CONSTRUÇÃO DE ÂNGULOS COMPLEMENTARES
Nesse vídeo, os estudantes constroem, no software Geogebra, um ângulo de 90°, além de uma semirreta interna. Esse momento evidenciou o entendimento dos estudantes a respeito dos procedimentos realizados e propiciou a formalização das definições de ângulos complementares. A professora utilizou a estratégia de circular na sala de modo a verificar o andamento da resolução da segunda questão, fazendo mediações para auxiliá-los. O indicado é que nesse momento o(a) professor(a) incentive os estudantes a moverem a semirreta para observarem que a soma dos ângulos é sempre 90°.
CONSTRUÇÃO DE ÂNGULOS SUPLEMENTARES
Nesse vídeo, os estudantes constroem no software Geogebra um ângulo de 180° e a semirreta interna ao ângulo. Esse momento evidenciou o entendimento dos estudantes a respeito dos procedimentos necessários para a construção do ângulo raso, além de apresentar a autonomia da estudante em verificar com a calculadora que a soma dos ângulos suplementares dá 180°. A professora utilizou a estratégia de verificar a resolução dos estudantes, fazendo mediações para auxiliá-los na compreensão da definição de ângulos suplementares. Sugerimos que o(a) professor(a), nesse momento, também incentive os estudantes a moverem a semirreta para observarem que a soma dos ângulos é sempre 180°.
SISTEMATIZANDO A SEGUNDA QUESTÃO
Nesse vídeo, a professora constrói na lousa exemplos análogos aos dos estudantes com a intenção de sistematizar a ideia de ângulos complementares e suplementares. Ela ressaltou que o valor de um ângulo sempre completa o valor do outro. Essa estratégia foi utilizada para que os estudantes percebessem as regularidades a partir das quais a professora pôde sistematizar os conceitos de ângulos complementares e suplementares. Sugerimos que ao esboçar os ângulos na lousa o(a) professor(a) utilize como referência as construções dos próprios estudantes, validando os valores e desenhos criados por eles no software Geogebra.